

Open the File tab, then select Options in the lower left corner.
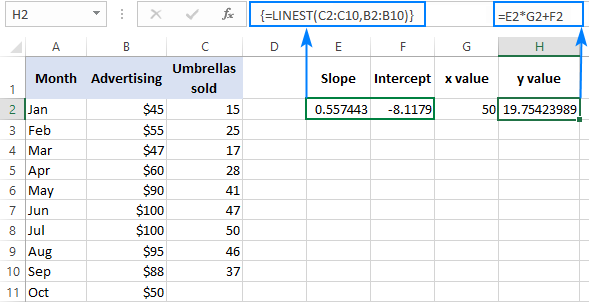
To enable the Analysis Toolpak, follow these steps: This add-in enables Excel to perform difficult statistical analysis, but it is not enabled by default in Excel installations. The final method for performing linear regression in Excel is to use the Analysis Toolpak add-in. Regression Analysis in Excel with the Analysis Toolpak Add-In But that’s a topic for a completely different post. Using Solver, you can fit whatever kind of equation you can dream up to any set of data. We can use this same concept to do more complex multiple linear regression or non-linear regression analysis in Excel. In the case of a simple linear regression like we have here, Solver is probably complete overkill. After all, we have just done “manually” what the Trendline tool and LINEST do automatically. Exactly what was predicted by the chart trendline and LINEST. When we click “Solve”, the Solver does its thing and finds that the values m = 165.36 and b = -79.85 define the best-fit line through the data. When properly set up, the solver dialog should look like this:
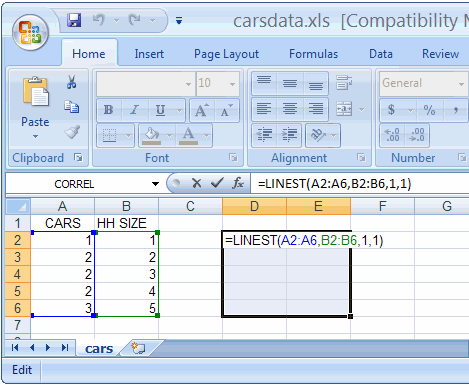
As a last step, uncheck the option to “Make Unconstrained Variables Non-Negative”. To do so, we will change variable cells E3 and F3, the slope and y-intercept of our linear equation. We want to minimize the objective, cell H3, or the sum of the squared errors. With the Solver open, the setup for this is pretty straightforward. You’ll find it way over on the right side of the ribbon: Follow the steps here to enable the Solver.Īfter the Add-In has been loaded, you can open the Solver from the Data tab. If you have never used the Solver Add-In before, you must first enable it. Next, enter some guess values for m and b into some cells on the worksheet. Let’s start again with the x- and y- data we had before. Use the Solver to find values of the slope and intercept that minimize the total error. Calculate the error between the calculated y-values and the y-data. Calculate new y-values based on those guess values. Enter “guess-values” for the slope and intercept of the equation. It will also introduce you to the possibilities for more complicated curve fitting using Excel. I’ve included it here because it provides some understanding into the way that the previous linear regression methods work. Fortunately, it will probably be unnecessary to ever use this method for simple linear regression. This method is more complex than both of the previous methods. That means we can use them dynamically in a calculation somewhere else in the spreadsheet. Completion of this course will give you an understanding of the concepts of the Bayesian approach, understanding the key differences between Bayesian and Frequentist approaches, and the ability to do basic data analyses.This was obviously more work than using a trendline, but the real advantage here is that the slope and y-intercept values have been output to a cell. The lectures provide some of the basic mathematical development as well as explanations of philosophy and interpretation. For computing, you have the choice of using Microsoft Excel or the open-source, freely available statistical package R, with equivalent content for both options. This course combines lecture videos, computer demonstrations, readings, exercises, and discussion boards to create an active learning experience. In particular, the Bayesian approach allows for better accounting of uncertainty, results that have more intuitive and interpretable meaning, and more explicit statements of assumptions. 
We will compare the Bayesian approach to the more commonly-taught Frequentist approach, and see some of the benefits of the Bayesian approach.
Calculate linear regression excel how to#
We will learn about the philosophy of the Bayesian approach as well as how to implement it for common types of data. This course introduces the Bayesian approach to statistics, starting with the concept of probability and moving to the analysis of data.








 0 kommentar(er)
0 kommentar(er)
